Tornado Cash Circuits - Overview

    2025, Nov 19
  • Withdrawal Mechanics: Proving Without Revealing
  • Why These Circuits Matter
  • Conclusion
  • Reference

    • Tornado Cash is one of Ethereum’s pioneering privacy protocols build on zk-SNARK and Circom zero-knowledge circuits

    • These circuits are the components that allow users to prove they deposited funds without ever revealing which deposit is theirs.

    This article summarizes how those circuits work, the underlying cryptographic components, and how Tornado Cash turns them into private deposits and withdrawals on-chain.

    Warning: this article is still in draft state and its content is still mainly taken from the Tornado cash documentation with a few edits of my own. Its content should become more personal later.

    [TOC]

    What Tornado Cash Circuits Do

    Tornado Cash uses a set of Circom ZK-SNARK circuits to prove several essential claims about a user’s deposit:

    • The deposit is valid and exists in the contract’s Merkle tree
    • The depositor has not withdrawn it before
    • The prover knows the secret values that created the deposit commitment
    • (Optionally) In anonymity mining, the circuit can also prove how long a note remained in the pool

    These capabilities let users obscure the link between their deposit and withdrawal — without trusting an intermediary.

    The ZK Foundations: SNARKs, Groth16, Circom, and snarkjs

    Tornado Cash is built on a specific zero-knowledge proving system:

    GROTH16 SNARKs, which offer:

    • Very small proofs
    • Fast on-chain verification
    • A trusted setup (required for efficiency)

    To build the circuits, Tornado Cash uses two essential tools:

    • Circom – a domain-specific language that compiles human-readable circuit logic into R1CS constraints and a witness generator.
    • snarkjs – a toolkit for trusted setup, proof generation, and verification.

    From Circuits to Constraints: R1CS, QAPs, and Witnesses

    R1CS: The mathematical backbone

    Circom compiles circuits into an R1CS (Rank-1 Constraint System) — a set of polynomial-like equations that the prover must satisfy. Each user input must generate a solution vector that satisfies every constraint.

    QAP: Polynomial transformation

    The R1CS is converted into a Quadratic Arithmetic Program, allowing all constraints to be checked simultaneously using polynomial commitments.

    Witness generation

    A witness is the complete set of intermediate values the circuit computes internally. The prover generates a witness from their private and public inputs — but only a tiny part of this becomes public.

    This makes the proof both valid and private.

    Tornado Cash Circuits in Practice

    Tornado Cash consists of two major circuit families:

    The Core Deposit Circuit

    Handles the privacy-preserving deposit system:

    • Users generate a Pedersen commitment from two secrets (a nullifier and a secret).
    • This commitment is inserted into a special MiMC-based Merkle tree.
    • No proof is generated at deposit time — only during withdrawal.

    Anonymity Mining Circuits

    Extend the core logic by proving how many blocks a note stayed deposited, rewarding users who keep funds locked longer.

    Deposit Mechanics: Commitments and Merkle Trees

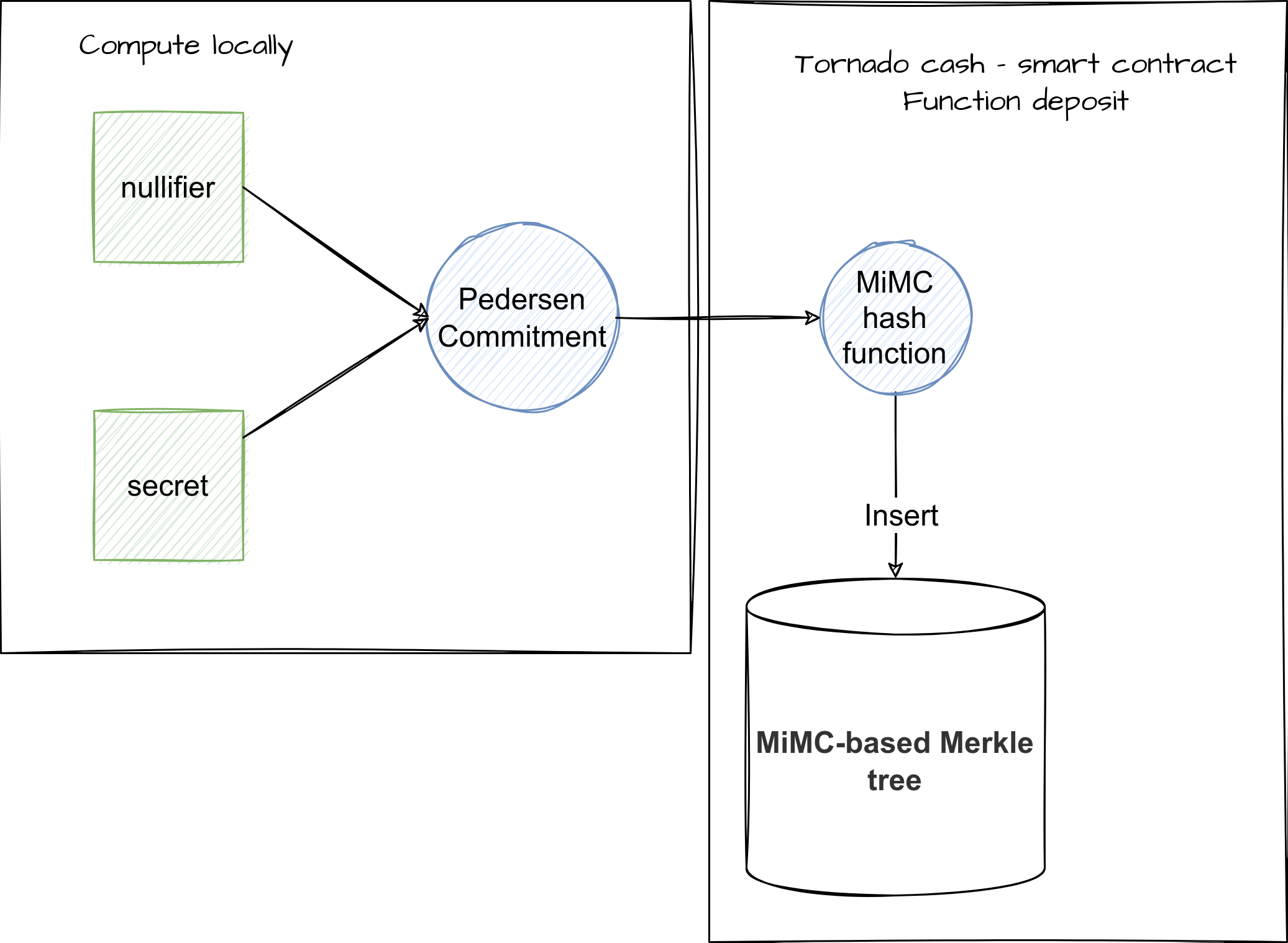
    tornado_cash_deposit.drawio

    Pedersen Commitments

    A deposit commitment is created from two 31-byte random values:

    1. Nullifier – later used to prevent double withdrawals
    2. Secret – protects the user’s anonymity

    These are concatenated and Pedersen hashed into a point on the Baby Jubjub elliptic curve — chosen because it is efficient inside SNARK circuits.

    MiMC Merkle Tree

    All commitments live inside a Merkle tree whose nodes are hashed using MiMC, a ZK-friendly hash. The contract stores a rolling history of 100 recent roots, used later for withdrawal proofs.

    Here are the circuits:

    HashLeftRight

    include "../node_modules/circomlib/circuits/mimcsponge.circom";

// Computes MiMC([left, right])
template HashLeftRight() {
    signal input left;
    signal input right;
    signal output hash;

    component hasher = MiMCSponge(2, 1);
    hasher.ins[0] <== left;
    hasher.ins[1] <== right;
    hasher.k <== 0;
    hash <== hasher.outs[0];
}

    Takes two inputs: left and right

    Feeds them into a MiMC sponge hasher as a 2-element input array

    Sets the MiMC key (k) to 0 (Tornado Cash uses MiMC with a zero key)

    Returns the resulting hash

    DualMux

    // if s == 0 returns [in[0], in[1]]
// if s == 1 returns [in[1], in[0]]
template DualMux() {
    signal input in[2];
    signal input s;
    signal output out[2];

    s * (1 - s) === 0
    out[0] <== (in[1] - in[0])*s + in[0];
    out[1] <== (in[0] - in[1])*s + in[1];
}

    DualMux is a multiplexer that swaps the inputs if s = 1.

    • If s = 0:

      out = [in[0], in[1]]

    • If s = 1:

      out = [in[1], in[0]]
    Why the constraint?
    s * (1 - s) === 0

    This enforces that s must be either 0 or 1 (a boolean).

    Why is this needed?

    In a Merkle proof each sibling is either on the left or right:

    If leaf is on the left: hash = MiMC(leaf, sibling)
If leaf is on the right: hash = MiMC(sibling, leaf)

    DualMux chooses the correct ordering using the selector bit s.

    MerkleTreeChecker

    Verifies that merkle proof is correct for given merkle root and a leaf pathIndices input is an array of 0/1 selectors telling whether given pathElement is on the left or right side of merkle path

    template MerkleTreeChecker(levels) {
    signal input leaf;
    signal input root;
    signal input pathElements[levels];
    signal input pathIndices[levels];

    component selectors[levels];
    component hashers[levels];

    for (var i = 0; i < levels; i++) {
        selectors[i] = DualMux();
        selectors[i].in[0] <== i == 0 ? leaf : hashers[i - 1].hash;
        selectors[i].in[1] <== pathElements[i];
        selectors[i].s <== pathIndices[i];

        hashers[i] = HashLeftRight();
        hashers[i].left <== selectors[i].out[0];
        hashers[i].right <== selectors[i].out[1];
    }

    root === hashers[levels - 1].hash;
}

    This is the core logic.

    Inputs:

    • leaf — the commitment hash being proven
    • root — the Merkle root being checked
    • pathElements[i] — sibling nodes at each tree level
    • pathIndices[i] — 0/1 values telling whether the leaf/sibling is on the left or right
    The loop performs:

    For each level of the tree:

    1. Select correct ordering of leaf & sibling
    selectors[i] = DualMux();
selectors[i].in[0] <== (previous hash or leaf)
selectors[i].in[1] <== pathElements[i];
selectors[i].s <== pathIndices[i];

    If pathIndices[i] == 0, order = [leaf, sibling] If pathIndices[i] == 1, order = [sibling, leaf]

    1. Hash them
    hashers[i] = HashLeftRight();
hashers[i].left <== selectors[i].out[0];
hashers[i].right <== selectors[i].out[1];

    This recomputes the Merkle parent node.

    1. fiinal check: does computed root = provided root?
    root === hashers[levels - 1].hash;

    If this equality does not hold, the circuit rejects the proof.

    This enforces:

    The prover knows a valid Merkle path from leaf to root.

    Withdrawal Mechanics: Proving Without Revealing

    Withdrawals are where Tornado Cash’s circuits are useful: users prove they deposited funds without revealing which leaf is theirs.

    The Circom circuit are not directly put on the blockchain, they are firstly transpiled into Solidity code and put, in the case of Tornado Cash, in the smart contract Verifier.sol .

    Here is the circuit:

    
include "../node_modules/circomlib/circuits/bitify.circom";
include "../node_modules/circomlib/circuits/pedersen.circom";
include "merkleTree.circom";

// computes Pedersen(nullifier + secret)
template CommitmentHasher() {
    signal input nullifier;
    signal input secret;
    signal output commitment;
    signal output nullifierHash;

    component commitmentHasher = Pedersen(496);
    component nullifierHasher = Pedersen(248);
    component nullifierBits = Num2Bits(248);
    component secretBits = Num2Bits(248);
    nullifierBits.in <== nullifier;
    secretBits.in <== secret;
    for (var i = 0; i < 248; i++) {
        nullifierHasher.in[i] <== nullifierBits.out[i];
        commitmentHasher.in[i] <== nullifierBits.out[i];
        commitmentHasher.in[i + 248] <== secretBits.out[i];
    }

    commitment <== commitmentHasher.out[0];
    nullifierHash <== nullifierHasher.out[0];
}

// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of deposits
template Withdraw(levels) {
    signal input root;
    signal input nullifierHash;
    signal input recipient; // not taking part in any computations
    signal input relayer;  // not taking part in any computations
    signal input fee;      // not taking part in any computations
    signal input refund;   // not taking part in any computations
    signal private input nullifier;
    signal private input secret;
    signal private input pathElements[levels];
    signal private input pathIndices[levels];
	
    component hasher = CommitmentHasher();
    
    // Commitment preimage (private)
    hasher.nullifier <== nullifier;
    hasher.secret <== secret;
    
    // Constraint: the user know the (public) nullifierHash preimage
    hasher.nullifierHash === nullifierHash;
	
    // Merkle Tree verifier
    component tree = MerkleTreeChecker(levels);
    // Leaf
    tree.leaf <== hasher.commitment;
    // Merkle root (public)
    tree.root <== root;
    for (var i = 0; i < levels; i++) {
        // Merkle proof (private)
        tree.pathElements[i] <== pathElements[i];
        tree.pathIndices[i] <== pathIndices[i];
    }

    // Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof
    // Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints
    // Squares are used to prevent optimizer from removing those constraints
    signal recipientSquare;
    signal feeSquare;
    signal relayerSquare;
    signal refundSquare;
    recipientSquare <== recipient * recipient;
    feeSquare <== fee * fee;
    relayerSquare <== relayer * relayer;
    refundSquare <== refund * refund;
}

component main = Withdraw(20);

    Source: github.com/tornadocash - withdraw.circom

    Summary tab

    Here’s a compact summary table of all signals and variables in the Circom code you provided:

    CommitmentHasher

    Signal / Variable Type Scope Description / Purpose
    nullifier input CommitmentHasher User’s secret nullifier for deposit note
    secret input CommitmentHasher User’s secret for deposit note
    commitment output CommitmentHasher Pedersen hash of nullifier
    nullifierHash output CommitmentHasher Pedersen hash of nullifier; prevents double-spending
    commitmentHasher component CommitmentHasher Pedersen hash component for full commitment
    nullifierHasher component CommitmentHasher Pedersen hash component for nullifier only
    nullifierBits component CommitmentHasher Converts nullifier into 248-bit array
    secretBits component CommitmentHasher Converts secret into 248-bit array

    Withdraw

    Signal / Variable Type Scope Description / Purpose
    root input Withdraw Public Merkle tree root for verification
    nullifierHash input Withdraw Public nullifier hash to prevent double-spending
    recipient input Withdraw Withdrawal recipient (anchored in proof)
    relayer input Withdraw Relayer address (anchored in proof)
    fee input Withdraw Relayer fee (anchored in proof)
    refund input Withdraw Refund to relayer (anchored in proof)
    nullifier private input Withdraw User’s private nullifier
    secret private input Withdraw User’s private secret
    pathElements private input Withdraw Merkle tree sibling nodes along path from leaf to root
    pathIndices private input Withdraw 0/1 selectors indicating left/right positions in Merkle path
    hasher component Withdraw Instance of CommitmentHasher to recompute commitment and nullifierHash
    tree component Withdraw Instance of MerkleTreeChecker to verify commitment inclusion
    recipientSquare signal Withdraw Squared value of recipient to bind it in proof constraints
    feeSquare signal Withdraw Squared value of fee to bind it in proof constraints
    relayerSquare signal Withdraw Squared value of relayer to bind it in proof constraints
    refundSquare signal Withdraw Squared value of refund to bind it in proof constraints
    main component Global Instantiates Withdraw circuit with 20-level Merkle tree

    Public inputs of a withdrawal proof

    • A recent Merkle root
    • The nullifier hash (prevents double spends)
    • Recipient & relayer addresses
    • Relayer fee and refund

    Private inputs include

    • The original nullifier and secret
    • The Merkle path elements
    • Left/right path selectors

    The circuit proves three things

    1. Nullifier Hash Check

    Confirms the nullifier is valid and matches the user’s original commitment.

    2. Merkle Path Validity

    Proves the user’s commitment exists somewhere in the Merkle tree whose root is publicly known — without showing where.

    3. Integrity of Withdrawal Parameters

    Ensures the relayer fee, recipient, and other parameters cannot be tampered with.

    Proof Generation and Verification

    After computing the witness, the prover generates a SNARK proof. The contract’s Groth16 verifier then checks:

    • Root is valid
    • Nullifier hasn’t been spent
    • Proof matches the public inputs
    • Relayer fee is within bounds

    If all checks pass, the withdrawal succeeds.

    Why These Circuits Matter

    Tornado Cash’s circuits enable:

    • Unlinkability: Withdrawals cannot be matched to deposits
      • Note that you can track deposit and withdrawal and try to match them. For example, if an address makes a deposit of 100 ether on a certain date and another address withdraw the same amount the day later, you can probably estimate that this is the same person behind the operation. See also SlowMist AML: Tracking funds laundered by Tornado Cash
    • Double-spend protection: Nullifiers prevent reuse
    • Efficiency: Groth16 proofs remain small and cheap to verify
    • On-chain privacy without trust: No mixers, no custodians, no intermediaries

    This combination makes Tornado Cash a foundational example of privacy engineering on Ethereum.

    Conclusion

    Tornado Cash’s circuit architecture transforms zero-knowledge cryptography into a practical, permissionless privacy tool. By combining Circom circuits, Pedersen commitments, MiMC hashing, and Groth16 proofs, it creates a system where users can prove they deposited funds — without ever revealing which deposit belongs to them.

    The result is one of the most influential and technically sophisticated privacy protocols in the blockchain ecosystem.

    Summary schema

    Here is a summary from the documentation:

    tornado_cash_diagram

    Reference

    Feel free to contact me on
    # solidity # ethereum # smart-contract

    Share button

    You might also enjoy

    Hypergraph and Hypertree - Overview

    Recurrent Neural Networks (RNNs) - Overview