Understanding zk-SNARK: A Deep Dive into Zero-Knowledge Proofs

    2025, Jul 29

    zk-SNARK stands for Zero-Knowledge Succinct Non-Interactive Argument of Knowledge.

    They were introduced in a 2012 paper co-authored by Nir Bitansky, Ran Canetti, Alessandro Chiesa, and Eran Tromer.

    It is a cryptographic technique that allows one party (the prover) to prove to another party (the verifier) that they know a piece of information, such as a secret key, without revealing the information itself.

    Zero-Knowledge Proof are widely used in blockchain technology to enhance privacy and/or scalability.

    Core properties:

    • Zero-Knowledge: No knowledge beyond the validity of the statement (validity of the claim) is revealed.
    • Succinct: The proofs are very small and quick to verify.
    • Non-Interactive: A single message from the prover is sufficient. The proof does not require back-and-forth communication between the prover and verifier after its generation.

    [TOC]

    zk-snark.drawio

    History

    ZK-SNARK is the result of several different innovation in the field of ZK, notably:

    • Zero-knowledge interactive proof systems (“The Knowledge Complexity of Interactive Proof Systems”, 1989).)
    • Non-interactive zero-knowledge (NIZK) proofs (NONINTERACTIVE ZERO-KNOWLEDGE (1991, pp. 1084–1118))
    • reducing the size of the proof sent.
    • make proofs constant size
    • Quadratic Span program (QSP) and Quadratic Arithmetic Program (QAP) reductions, where an NP-statement is reduced to a statement about QSPs
    • The Pinocchio protocol and Groth16

    Zero-Knowledge interactive proof protocols were the starting point of zk-SNARKs.

    Reference and more details in this publication: arxiv.org - A Review of zk-SNARKs

    Key Components of zk-SNARK

    Arithmetic circuits

    zk-SNARKs work by transforming computations into arithmetic circuits. Each computation step becomes part of a mathematical representation.

    A function f(x) is represented as a sequence of arithmetic operations (additions and multiplications). Each gate has constraints on its inputs and output.

    An arithemetic circuit is:

    • Direct acyclic graph (DAG) where
      • internal nodes are labeled +,-, or x
      • Inputs are labeled 1,x1, ….,xn
    • Defines an n-variate polynomial with an evualation recipe
    • Fix a finite Field

    [\begin{aligned} F = {0,…, p-1} ~for~some~prime~p >2 \end{aligned}]

    \(\begin{aligned} C: F^n - >F \end{aligned}\) Example:

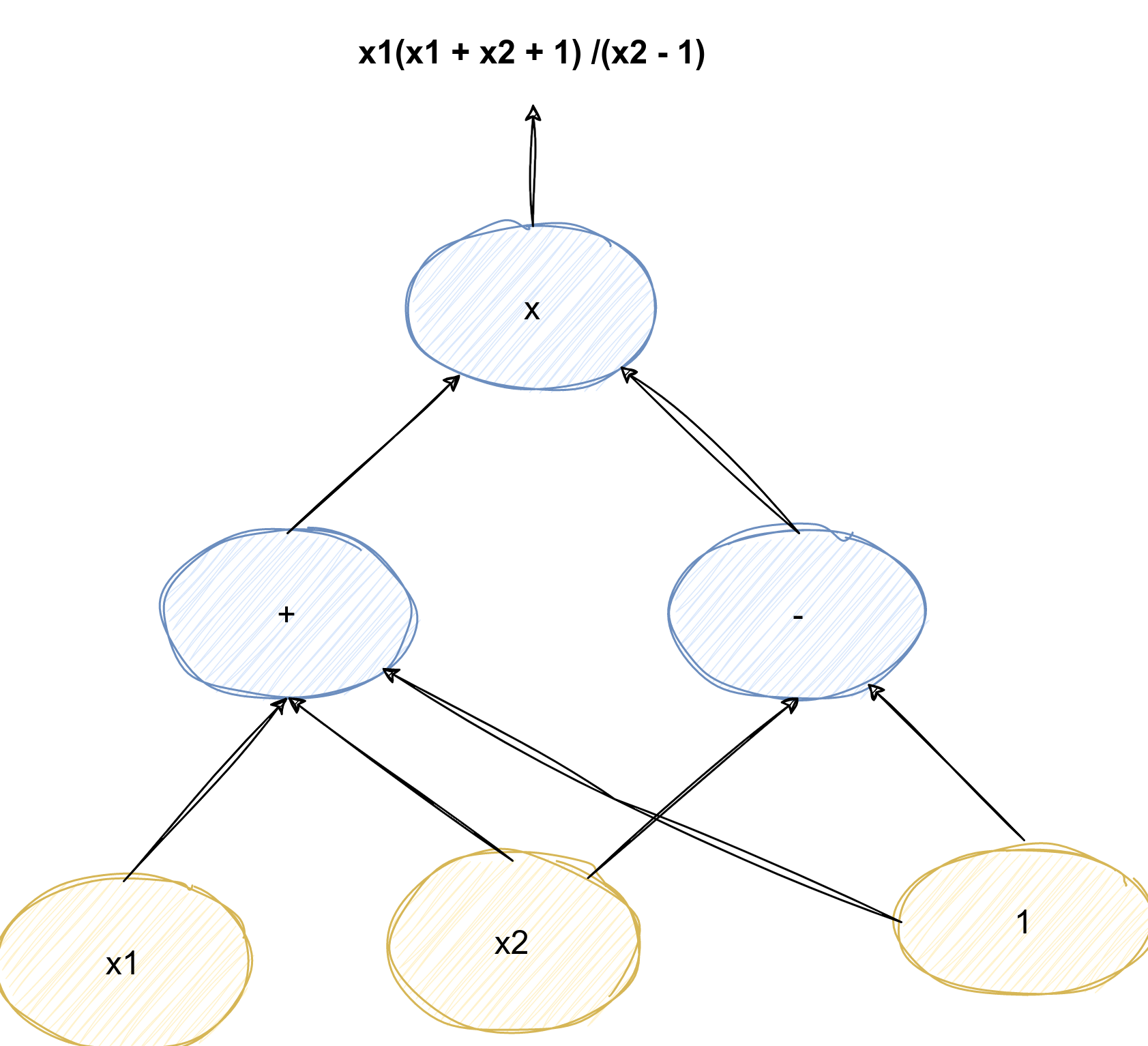
    zk-snark-arithmetic-circuit.drawio

    Reference: rdi.berkeley.edu - Lecture2-2023.pdf, page 18

    Structured vs. unstructured circuits

    • An unstructured circuit: a circuit with arbitrary wires
    • A structured circuit

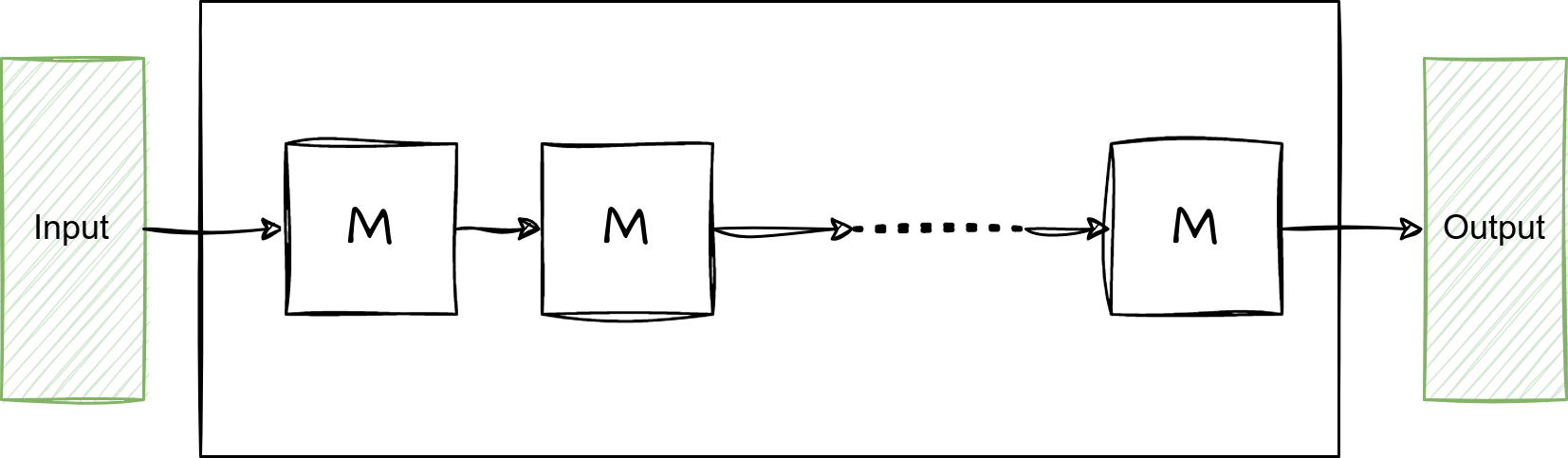
    zk-snark-structured-circuit.drawio

    M is often called virtual Machine (VM) – one step of a processor

    Some SNARK techniques only apply to structured circuits

    Reference: rdi.berkeley.edu - Lecture2-2023.pdf, page 20

    NARK: Non-interactive ARgument of Knowledge (preprocessing)

    A preprocessing NARK is a triple (S, P, V):

    • S(C) -> public parameters (pp, vp) for prover and verifier
    • P(PP, x, w) -> Proof π
    • V(vp, x, π) -> accept or reject

    where

    • x is a public statement in Fn

    • w is a secret witness in F^m

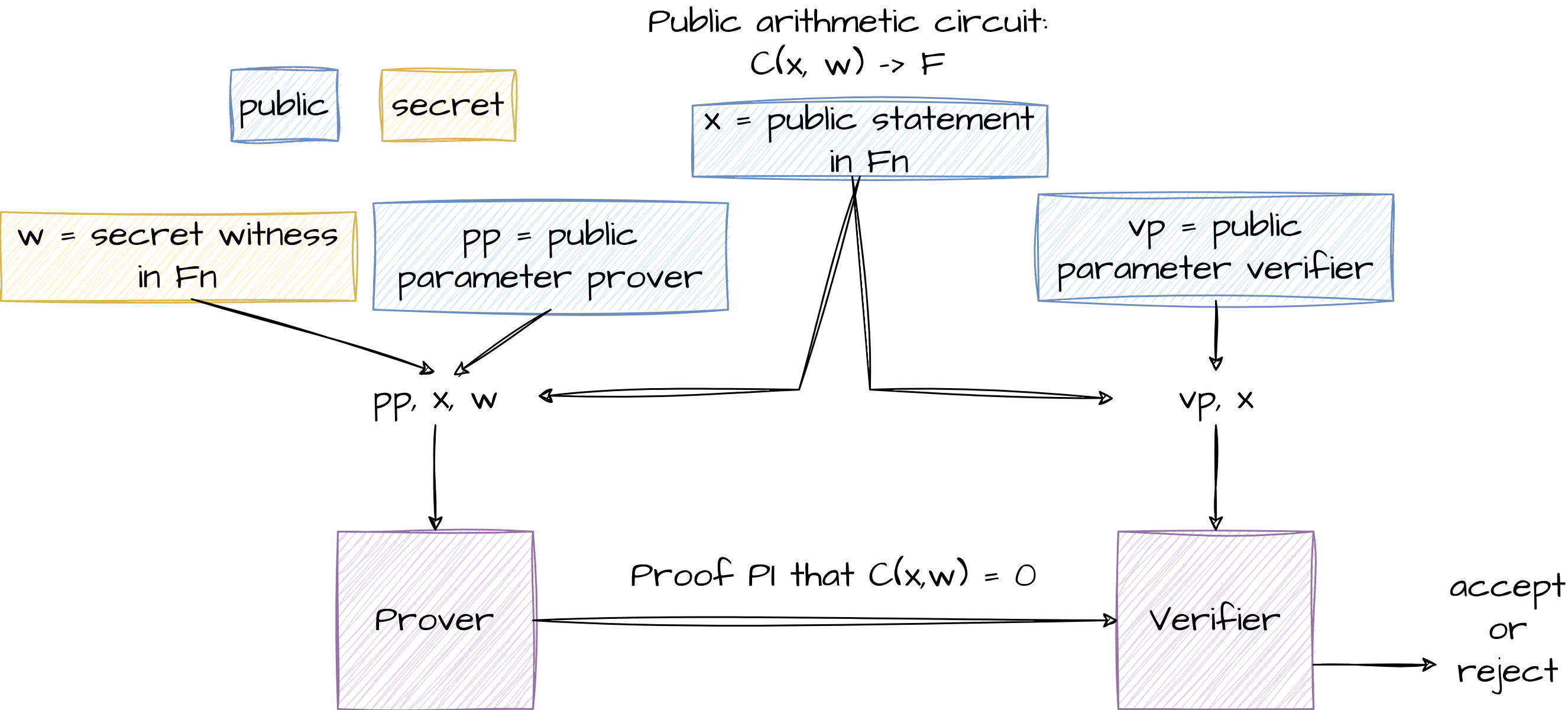
    zk-snark-NARK.drawio

    Reference: rdi.berkeley.edu - Lecture2-2023.pdf, page 21

    SNARK: a Succinct ARgument of Knowledge

    Succinct

    A succinct preprocessing NARK is a triple (S, P, V):

    • S(C) -> public parameters (pp, vp) for prover and verifier
    • P(PP, x, w) -> short Proof π

    [\begin{aligned} len(PI) = sublinear(|w|) \end{aligned}]

    • V(vp, x, π) -> fast to verify

    [\begin{aligned} time(V) = O_\lambda(|x|), sublinera(|C|) \end{aligned}]

    Example sublinera function \(\begin{aligned} f(n) = \sqrt(n) \end{aligned}\)

    Reference: rdi.berkeley.edu/zk-learning/assets/Lecture2-2023.pdf, page 24

    Strongly succinct

    A strongly succinct preprocessing NARK is a triple (S, P, V):

    • S(C) -> public parameters (pp, vp) for prover and verifier
    • P(PP, x, w) -> short Proof π

    [\begin{aligned} len(π) = log(|C|) \end{aligned}]

    • V(vp, x, π) -> fast to verify

    [\begin{aligned} time(V) = O_\lambda(|x|), log(|C|) \end{aligned}]

    Reference: rdi.berkeley.edu/zk-learning/assets/Lecture2-2023.pdf, page 25

    Types of preprocessing Setup (trusted setup)

    The Trusted Setup is a crucial step where parameters are generated. These parameters are public and enable the creation of proofs, but their security depends on the assumption that the private “toxic waste” from the setup remains undisclosed. “As such, trusted setups are commonly run with many participants to render the possibility of this occurrence low enough.”

    Recall setup for circuit C: S(C) -> public parameters (Sp, Sv)

    zk-snark-preprocessing-setup

    Trusted setup per circuit

    S(C) uses data that must be kept secrets

    If the trusted setup is compromises => can prove false statements

    Trusted but universal (updatable) setup

    • secrets in S(C) are independent of C

    [\begin{aligned} S = (S_{init}, S_{pre}) \end{aligned}]

    Transparent setup

    S(C) does not use secret data (no trusted setup)

    Reference: rdi.berkeley.edu/zk-learning/assets/Lecture2-2023.pdf, page 28

    Snark and zk-snark difference

    SNARK: a NARC (complete and knowledge sound) that is succinct

    zk-SNARK: a SNARK that is also zero knowledge

    Quadratic Arithmetic Programs (QAPs)

    These express the circuit’s constraints, which must be satisfied to verify the proof.

    A QAP encodes the correctness of the circuit into polynomial form. For a valid computation, the polynomials P(x), Q(x), and Z(x) must satisfy: \(\begin{aligned} P(x) \cdot Q(x) = h(x) \cdot Z(x) \end{aligned}\) Where:

    • P(x), Q(x): Encoded left and right input polynomials.
    • Z(x): Target polynomial (vanishing polynomial).
    • h(x): Witness polynomial (proof that computation is correct).

    Pairing-Based Cryptography

    zk-SNARKs use elliptic curve pairings to create verifiable commitments. Given two cyclic groups G1 and G2, and a bilinear pairing e:G1×G2→GT : we have: \(\begin{aligned} e(aP, bQ) = e(P, Q)^{ab} \end{aligned}\) This property is used to verify polynomial relationships without revealing the witness.

    Applications of zk-SNARKs

    Outsourcing computation

    zk-SNARKs can compress complex computations into verifiable proofs, reducing the load on verifiers in distributed systems.

    Outsourcing computation: (no need for zero knowledge):

    L1 chain quickly verifies the work of an off-chain service

    Examples:

    • Scalability: proof-based Rollups (zkRollup) off-chain service processes a batch of Tx;
      • L1 chain verifies a succinct proof that Tx were processed correctly
    • Bridging blockchains: proof of consensus (zkBridge) enables transfer of assets from one chain to another

    Reference:

    zk-learning - zk-learning/assets/Lecture2-2023.pdf

    Privacy

    zk-SNARKs are prominently used in cryptocurrencies like Zcash, allowing users to hide transaction details while still ensuring their validity.

    Some applications require zero knowledge (privacy):

    • Private Tx on a public blockchain:
      • zk proof that a private Tx is valid (Tornado cash, Zcash, IronFish, Aleo)
    • Compliance:
      • Proof that a private Tx is compliant with banking laws (Espresso)
      • Proof that an exchange is solvent in zero-knowledge (Raposa)

    other use in public blockchain: tornado cash, IronFish + Aleo (private Dapps)

    ZCash - Halo2

    With Network Upgrade 5 (NU5) in May 2022, Zcash introduced the Orchard shielded payment protocol, which utilizes the Halo 2 zero-knowledge proving system.

    Halo is a new zk-SNARK that’s finally capable of solving two outstanding issues in Zcash:

    • Removing the trusted setup while hitting performance targets
    • Supporting a scalable architecture for private digital payments.

    Zcash was the first widespread application of zk-SNARKs, applying the technology to create shielded transactions in which the sender, recipient, and amount are kept private. Shielded transactions in Zcash can be fully encrypted on the blockchain yet still be verified as valid under the network’s consensus rules by using zk-SNARKs. zk-snarks-vs-zk-starks

    Reference: Learn zcash - WHAT ARE ZK-SNARKS?

    Mina - Pickles

    Mina Protocol is a layer 1 zk-blockchain which uses a type of zk-SNARKs called Pickles.

    Pickles supports concept of recursion — that a proof can refer to itself — and doing this doesn’t increase the size of the proof, no matter how many times we refer to the initial one. That recursion, or picture of a picture, is what allows Mina to stay small.

    Reference: Mina Protocol - What are zk-SNARKs?, Mina Protocol - A Guide to zk-SNARKs

    Compliance & Identity Verification

    Enables proving identity attributes (e.g., age or citizenship) without revealing detailed personal data.

    Who Use snark

    –> To do

    Atzec - Plonk

    Comparison with Other Zero-Knowledge Systems

    Feature zk-SNARK zk-STARK Bulletproofs
    Proof Size Very small O(1) Larger than zk-SNARK
    O(logn)    		 Larger than zk-SNARK
    O(logn)
    Verification Speed Extremely fast O(1) Slower than zk-SNARK
    O(logn)    		 Comparable
    Slower O(n)
    Trusted Setup Required Not required Not required
    Scalability High Very high Moderate
    Quantum Resistance ❌
    Vulnerable to quantum attacks    		 ✅Resistant ⚠️Partially resistant

    • zk-STARK (Zero-Knowledge Scalable Transparent Arguments of Knowledge) removes the need for a trusted setup and is quantum-resistant. However, zk-STARK proofs are larger and slower to verify.

    • Bulletproofs, on the other hand, are non-interactive and efficient but lack succinctness for highly complex computations.

    Security of zk-SNARKs Against Quantum Computers

    The security of zk-SNARKs relies on cryptographic primitives like elliptic curve pairings and discrete logarithms. These problems are computationally hard for classical computers but susceptible to attacks by quantum computers, particularly with Shor’s algorithm. A sufficiently powerful quantum computer could compromise the integrity of zk-SNARK-based systems.

    In contrast, zk-STARKs use hash-based cryptographic techniques, making them inherently resistant to quantum threats.

    As the development of quantum computers progresses, systems based on zk-SNARKs will need to transition to quantum-secure alternatives to maintain their security guarantees.

    Scheme

    It exists several different proving schemes. Here a quick list:

    Scheme Curves Setup Post-quantum
    G16 ALTBN_128, BLS12_381 trusted per circuit no
    GM17 ALTBN_128, BLS12_381, BLS12_377, BW6_761 No universal ?
    Marlin ALTBN_128, BLS12_381, BLS12_377, BW6_761 universal trusted setup no
    Bulletproofs   Transparent no
    STARK   Transparent Yes
    • All schemes have a circuit-specific setup phase called setup.
    • Universal schemes also feature a preliminary, circuit-agnostic step called universal-setup. The advantage of universal schemes is that only the universal-setup step requires trust, so that it can be run a single time and reused trustlessly for many programs.

    Reference: zokrates.github.io - proving_schemes.html, Schemes, rdi.berkeley.edu/zk-learning/assets/Lecture2-2023.pdf, page 29

    Variant

    SNARKs

    Plonk

    Universal and Updateable Trusted Setup

    PLONK requires a trusted setup procedure. In a trusted setup, a set of initial parameters is generated, and the security of the scheme depends on keeping these parameters secret.

    • PLONK’s trusted setup is universal and updateable. This means that instead of needing a separate trusted setup for each program to be proven, there is one single trusted setup that can be used with any program (up to a certain maximum size defined during setup).
    • The trusted setup can involve multiple parties, and it remains secure as long as at least one of the participants is honest.
    • This multi-party procedure is sequential, allowing participants to be added over time, which increases the safety of the setup in practice.

    PLONK relies on a single standardized component called a polynomial commitment.

    • Polynomial commitments are cryptographic tools that enable efficient verification of polynomial equations.
    • PLONK uses Kate commitments, which are based on trusted setups and elliptic curve pairings. However, the scheme is flexible, allowing alternative schemes like FRI or DARK to be used instead.
    • This means that different trade-offs between proof size and security assumptions can be achieved by swapping out the polynomial commitment scheme.

    Reference: zkplabs - Introduce PLONK: Revolutionizing ZK-SNARK Technology for Efficiency and Privacy

    Conclusion

    zk-SNARKs enables privacy-preserving, efficient, and scalable solutions across various domains.

    However, the reliance on trusted setups and their vulnerability to quantum computers are notable challenges. zk-STARKs and Bulletproofs offer alternatives with distinct trade-offs.

    Future advancements in quantum-resistant algorithms and decentralized trusted setups will likely be the main point for the evolution of zk-SNARKs.

    Library

    See my article for more details: Overview of Zero-Knowledge development framework

    Library Maintainer Language Description
    zokrates   Rust ZoKrates is a toolbox for zkSNARKs on Ethereum. It helps you use verifiable computation in your DApp, from the specification of your program in a high level language to generating proofs of computation to verifying those proofs in Solidity.
    Gnark Consensys Go gnark is a fast zk-SNARK library that offers a high-level API to design circuits.
    rapidsnark) iden3 C++ Rapidsnark is a fast zkSNARK prover, that generates proofs for circuits created with circom and snarkjs.
    Nova Microsoft Rust Nova is a high-speed recursive SNARK , and a recursive SNARK enables producing proofs that prove statements about prior proofs).
    Plonky2 Polygon Zero Rust SNARK implementation based on techniques from PLONK and FRI.

    Reference

    Further reading

    Feel free to contact me on
    # zeroknowledge # zkp # zk-snark

    Share button

    You might also enjoy

    Hypergraph and Hypertree - Overview

    Tornado Cash Circuits - Overview

    Recurrent Neural Networks (RNNs) - Overview